고정 헤더 영역
상세 컨텐츠
본문

|
소성이론은 훅의 법칙이 적용되는 범위를 넘어선 변형률 범위에서 배로의 변형 거동을 취급하는 학문이다. 소성변형 |
|
그림 1. 연성재료의 대표적인 진응력-변형률 곡선 항복응력σ0까지는 훅의 법칙이 성립하고(이 σ0의 값은 변형률의 측정정확도에 크게 의존한다.), σ0를 지나면 금속은
σ = kεn 여기서 k는 ε = 0.1에서의 응력이고, n은 가공경화지수이며, 이 식을 log-log관계로 표시하였을 때의 기울기이다. |
|
진변형률과 공칭변형률 사이에는 다음과 같은 관계식이 성립한다. 진응력은 한 순간에서의 하중을 그것이 작용하는 단면적으로 나눈 값인데 비햐여 공칭응력은 그 하중을 초기의 단면 진응력은 공칭응력과 다음과 같은 관계를 가지고 있다. 체적일정 조건으로부터 |
|
◆ Von Mises조건 주응력이 어떤 combination이 critical값에 도달하면 항복한다. 즉, 둘째 응력불변량 J2가 어떤 일정값에 도달하면 항복이 일어난다.
단순인장일 경우를 생각해 보면
즉,
또, 순전단응력(torsion)일 때를 고려하면
인장일 때와 toersion일 때를 비교하면
Von Mises는 원래 이 조건식을 간단한 수학적 간단화를 위해서 제안하였으나, 후에 변형에너지가 어떤 일정한 값에 도달할 때 항복이 일어난다는 조건과 같은 의미를 가징다는 것을 증명하였다. |
|
◆ Tresca 조건(최대전단응력 조건식) 이 항복 조건은 최대 전단응력이 단순 인장시험에서의 전단항복응력 값에 도달할 때 항복이 일어난다는 것이다. 즉, 이다. 단순인장일때는 이고, 순전단응력일때는 이다. 최대 전단 응력조건은 Von Mises조건에 비하여 수식적으로 간단하고, 그 대문에 공학적 설계에 많이 이용된다. |
|
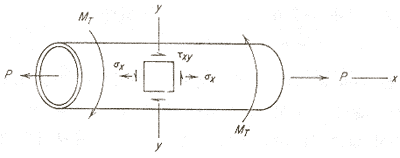
단순인장과 비틀림을 제외한 응력상태에서 항복에 대한 연구는 주로 박육원통(thin-wall tube)에서 행해져 왔다.
그림 2. 인장과 비틀림을 받고 있는 박육원통 최대전단응력항복조건은 다음과 같이 주어진다. 변형에너지 항복이론은 아래와 같이 표시한다. 두 식은 다같이 타원식이다. |
|
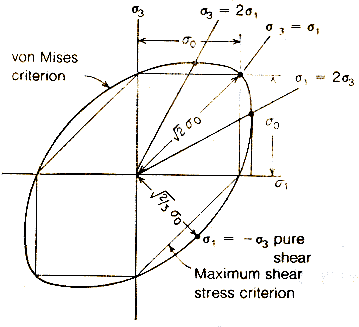
그림 3. 평면 응력상태에서 항복조건의 비교 이축 응력 조건
이 것은 장방경이 최대 전단 응력 조건에 대한 항복 곡선은 Mises의 그것 내에 들어간다. 두 항복 조건은 단순 인장과 등이축 응력 상태(σ1 = σ3)에서 일치한다. |
|
탄성 변형률이 무시되는 이상적인 소성체에 대한 응력-변형률 관계를 흐름의 법칙 혹은 Levy - Mises 식이라 부른다. 소성변형에서는 부피변화가 없다고 가정하면
이다 단순인장의 경우 σ1 ≠ 0, σ2 = σ3 = 0 그리고 σm = σ1/3 이고,
이다 . 이것과 체적 불변의 조건으로부터 Levy - Mises의 일반식을 얻을 수 있다.
이 식은 변형이 진행하는 순간 하나의 주응력 방향에서의 편차응력에 대한 변형률 증분의 비는 일정하다는 개념을 의미한다. 여기서 effective stress
이라고 정의하고 effective strain
이라고 했을 때 Levy-Mises 식은
으로 표현할 수 있다 |
'Learning > Engineering' 카테고리의 다른 글
| Tacoma Narrows Bridge Collapse "Gallopin' Gertie" [타코마다리] (0) | 2011.08.05 |
|---|---|
| 응력-변형도 선도 (0) | 2010.10.29 |
| 진응력(true stress) 진변형률(true strain) (1) | 2010.10.29 |
| 공학 영어 (0) | 2010.10.26 |
| 인장시험, Tensile Test (2) | 2010.10.25 |
| 탄성계수 (0) | 2010.10.22 |
| 스프링 탄성계수에 대한 정리 (0) | 2010.10.13 |


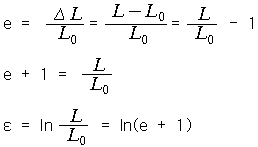
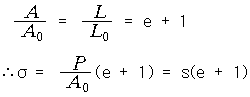
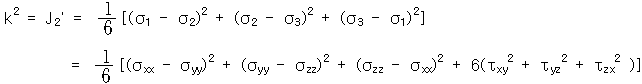

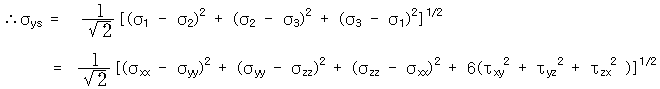
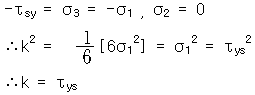
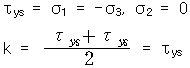
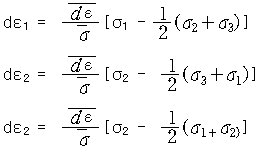





댓글 영역